| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- Negative Sampling
- Ai
- ANNOY
- word2vec
- 부스트캠프 AI Tech
- ALS
- wavenet
- BOJ
- Noise Contrastive Estimation
- Implicit feedback
- TTS
- matrix factorization
- FastSpeech2
- SGNS
- Neural Collaborative Filtering
- Dilated convolution
- CF
- Tacotron2
- NEG
- 논문리뷰
- RecSys
- Item2Vec
- Collaborative Filtering
- FastSpeech
- 추천시스템
- 백준
- CV
- Skip-gram
- Tacotron
- Recommender System
- Today
- Total
devmoon
[논문 리뷰] BPR: Bayesian Personalized Ranking from Implicit Feedback 본문
[논문 리뷰] BPR: Bayesian Personalized Ranking from Implicit Feedback
Orca0917 2022. 12. 6. 22:55ABSTRACT
아이템 추천이라는 작업은 아이템 목록에서 유저의 선호도에 맞추어 좋아할 만한 아이템들을 추천하는 것을 말한다. 저자들은 그런 추천 시스템을 만들기 위해 Implicit Feedback을 사용하였다. 물론 기존에도 Implicit Feedback을 사용하여 아이템 추천을 하는 Matrix Factorization (MF)이나 k-nearest-neighbor (kNN) 모델이 존재했었다. 하지만 이 2가지 모델들은 아이템을 추천할 때, 유저의 선호도에 맞추어 아이템들에 ranking을 매기고자 했는데 학습과정에서 ranking을 직접 최적화하는 부분이 없다는 한계가 있었다.
이에 저자들은 BPR-OPT 라는 새로운 최적화 방법을 소개한다. BPR-OPT는 베이즈 이론에서 등장하는 사후 확률을 최적화하는 방식으로 동작한다. 여기에 그치지 않고 저자는 LEARN-BPR이라는 학습 알고리즘도 같이 소개하는데, bootstrap 샘플링을 하는 SGD에 기반을 두고 있다. 최종적으로는 BPR-OPT과 LEARN-BPR을 통해서 이미 좋은 성능을 보여주고 있던 MF계열의 여러 모델들과 kNN을 성공적으로 뛰어넘어서 좋은 모습을 보여주었다고 밝힌다. 따라서, BPR을 하나의 모델이라기 보다 기존의 모델을 최적화하는 새로운 방법이라고 본다.
INTRODUCTION

추천시스템은 현대에 와서 정말 중요한 요소로 자리 잡고 있다. 온라인 쇼핑을 할 때와 유튜브나 넷플릭스와 같은 영상 콘텐츠를 소비할 때, 사용자와 서비스 공급자 모두에게 중요한 역할을 한다. 사용자는 질 좋은 서비스를 받을 수 있고, 공급자는 이로 인한 수익 창출이 발생할 수 있다. 그러기 위해서는 유저의 선호도를 알아야만 하는데, 유저 선호도는 유저가 과거에 어떤 상품을 구매했는지, 어떤 영상들을 시청했는지의 기록들을 이용해서 파악하는 것이 가능하다.
이런 높은 중요도로 인해 연구분야에서도 추천시스템에 대한 여러 실험들이 진행됐었다. 특히 유저가 직접 기록을 남긴 평점이나 좋아요, 싫어요와 같은 반응인 Explicit Feedback을 사용한 실험들이었다. 하지만 실제 세상에는 유저들이 직접 남긴 기록보다는 간접적으로 어떤 페이지를 방문하고 어떤 영상을 봤는지의 기록인 Implicit Feedback이 훨씬 많은 것이 사실이다. 또한 대부분의 서비스에서 이미 서버에 이런 기록들을 남기고 있기 때문에 추천 시스템을 도입하여 적용하기 용이하였다.
이번 논문을 통해 발표하고 싶은 것은 개인화된 선호도 랭킹을 매기는 일반적인 방법이며 주요 내용은 다음 4가지가 있다.
[1] 보편적으로 최적화할 수 있는 방법으로, 사후확률을 최대화하는 BPR-OPT에 대해 소개하고 AUROC를 최대화하는 것과 어떤 유사성이 있는지를 보여준다.
[2] BPR-OPT를 최대화하면서 학습하는 알고리즘인 LEARN-BPR을 소개한다. BPR-OPT를 학습하는데 있어서 기존의 경사 하강법보다 LEARN-BPR이 뛰어남을 보여준다.
[3] LEARN-BPR을 BPR-OPT뿐만 아니라 기존의 SOTA였던 MF와 kNN에 적용하는 방법을 소개한다.
[4] 실험을 통해 개인화된 추천에 있어서 기존의 다른 모델들보다 BPR-OPT를 사용해 최적화한 모델이 뛰어남을 보여준다.
RELATED WORK
기존에 추천시스템에서 가장 유명한 모델은 kNN CF였다. kNN CF에서 유사도 행렬을 계산할 때 사용되는 함수는 대충 어림짐작하여 "피어슨 유사도" 또는 "코사인 유사도"를 사용했었다. 이런 단순함에서 벗어나 최근에는 유사도 행렬을 오히려 모델의 파라미터로 설정하여 학습할 수 있게 만들었다.
kNN CF와 더불어 추천 시스템에서 implicit feedback과 explicit feedback 모두 강한 성능을 보여주는 MF가 있다. MF는 Singular Value Decomposition (SVD)라는 방법으로 학습이 되는데, 이 방법은 굉장히 과적합 되기 쉽다는 단점이 있었다. 따라서 과적합을 피하기 위해 사람들은 Regularization 규제화를 두어 문제를 피하였다.
공통적으로 위의 kNN과 MF는 유저의 선호도를 기반으로 좋아할 만한 아이템을 추천하게 되는데 문제는 그 어떤 방법도 직접 유저 선호도에 따른 아이템 랭킹에 초점을 맞춘 모델 파라미터를 수정하지 않는다는 것이다. 대신에 저 모델들이 학습하는 것은 유저가 특정 아이템을 선택했느냐 선택하지 않았냐의 정보였다. 따라서 저자는 새로운 학습 방법을 이 모델들에 적용해서 개선을 하는 모습을 보여주려고 한다.
PERSONALIZED RANKING
개인화된 랭킹문제는 유저에게 아이템 집합에 대해 랭킹을 주어 아이템을 추천하는 문제이다. 이 논문에서는 Implicit Feedback에 초점을 맞추어서 개인화된 선호도를 학습하게 할 것인데 저자는 이 Implicit Feedback의 특징을 발견한다. 그리고 Implicit Feedback이 없는 유저-아이템 쌍은 다음 2가지로 해석할 수 있다는 점에 초점을 맞추어 문제를 풀어나간다.
- 실제로 유저가 해당 아이템을 사기 싫어서 상호작용하지 않은 경우
- 사실 유저가 해당 아이템을 좋아하지만, 존재 자체를 몰라서 상호작용을 못했던 경우
Formalization
$U$를 모든 유저의 집합이라 하고 $I$를 모든 아이템의 집합이라고 한다면, Implicit Feedback을 $S$라고 했을 때, $S \subseteq U \times I$로 표현할 수 있다. 이제부터는 유저 $u$의 선호도에 따른 아이템 ranking을 기호로 $>_u$ 로 표현하며 아래의 3가지 조건을 모두 만족해야 한다.
\begin{align*}
&\forall_{i, j} \in I : i \neq j \Rightarrow i >_u j \vee j >_u i & (totality&)\\
&\forall_{i, j} \in I : i >_u j \wedge j >_u i \Rightarrow i = j & (antisymmetry&)\\
&\forall_{i, j, k} \in I : i >_u j \wedge j >_u k \Rightarrow i >_u k & (transitivity&)
\end{align*}
또한, 유저가 상호작용한 아이템 집합과 아이템과 상호작용한 유저들의 집합을 아래와 같이 정의하였다.
\begin{align*}
I_u^+ &:= \{ i \in I : (u, i) \in S \}\\
U_i^+ &:= \{ u \in U : (u, i) \in S \}
\end{align*}
Analysis of the problem setting
앞서 언급했듯이, Implicit Feedback은 '상호작용 했다'의 정보만 있을 뿐 유저가 어떤 아이템들을 싫어하는지의 정보는 알 수 없다. 이런 문제를 가장 잘 다룰 수 있는 것은 오로지 상호작용한 정보만 데이터로 쓰는 것이다. 하지만 이렇게 되면 머신러닝 모델들은 어떤 아이템들을 싫어하고 좋아하는지를 구분할 수 없기 때문에 문제가 생겨버린다.
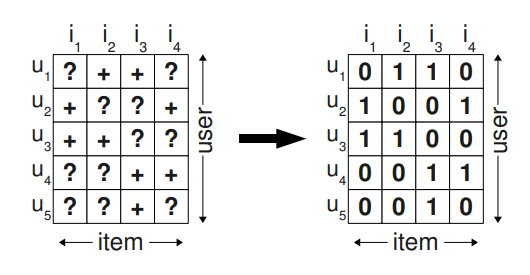
이에 추천 시스템 연구자들은 유저가 아이템을 얼마나 선호하는지에 대한 변수 $\hat{x}_{ui}$를 설정하여 모델이 학습하도록 만들었다. 그리고 이 선호도 점수를 기준으로 정렬하여 최종적으로 유저에게 추천되는 아이템이 무엇인지 상위에서부터 골라내면 되었다. 따라서 학습 데이터로는 $(u, i) \in S$로 상호작용 데이터가 있는 유저-아이템 쌍들을 1로, 나머지 상호작용하지 않은 모든 아이템 쌍 $(U \times I) \setminus S$을 0으로 설정하였다.
이렇게 해도 문제가 있었는데, 유저에게 추천해야 할 아이템 즉, 유저가 아직 상호작용하지 않은 아이템들이 학습 데이터로 들어갈 때 모두 0인 값으로 들어간다는 것이다. 학습 자체를 상호작용하지 않은 아이템들에 대해서는 0으로 예측하도록 만들었으니 당연히 올바른 결과를 얻어낼 수가 없는 것이다. 따라서 대부분의 머신러닝 모델들이 Regularizer를 도입하여 학습을 하는 것이 이런 이유에서다.
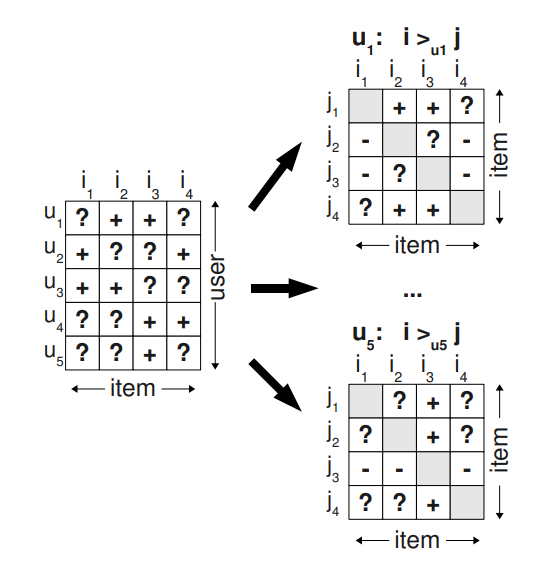
저자는 여기에 새로운 방향을 제시하였다. 유저의 아이템에 대한 선호도 랭킹 $>_u$를 재정의하는 것이다. 만약 $u$가 $i$와 상호작용한 이력이 있다면, 상호작용하지 않은 다른 아이템들보다 더 선호한다는 의미로 해석한다. 위의 그림에서 왼쪽 행렬을 보면, $u_1$은 $i_2$와는 상호작용한 기록이 있지만, $i_1$과는 상호작용하지 않았다. 따라서 $i_2 >_u i_1$으로 볼 수 있다. 이를 좀 더 수식화해서 나타내기 위해 학습 데이터 $D_S$를 아래와 같이 정의한다.
$$ D_S := \{ (u, i, j) \vert i \in I_u^+ \wedge j \in I \setminus I_u^+ \} $$
다시 말해, $(u, i, j)$가 의미하는 것은 $u$가 $i$를 $j$보다 선호함을 말한다. 이런 식으로 Implicit Feedback을 해석하게 되었을 때, 저자는 2가지 이득을 취할 수 있다고 한다. 첫 번째로, 학습 데이터에 상호작용한 아이템과 상호작용하지 않은 아이템 쌍이 모두 포함되게 된다. 나중에 추론해야 하는 데이터는 상호작용하지 않은 아이템 쌍인데 이는 학습 데이터셋과는 겹치는 부분이 존재하지 않아 학습에 효과적이다. 두 번째, 학습하는 데이터셋에서 $(u, i, j)$의 의미를 담아 유저 선호도에 따른 아이템 ranking을 반영할 수 있게 된다.
BAYESIAN PERSONALIZED RANKING (BPR)
이 파트에서는 개인화된 ranking을 최적화 하지 않았던 문제를 해결할 수 있는 일반화된 방법에 대해 소개한다. 정확히는 베이즈 정리에서 등장하는 가능도(likelihood)와 사전 확률(prior)을 사용하여 만든 최적화 함수인 BPR-OPT에 대한 이야기이다. 여기서 가능도는 $p(i >_u j \vert \Theta)$로 표시하고, 사전 확률은 $p(\Theta)$로 해석할 수 있으며 관련된 더 자세한 내용은 아래에서 다룬다. 또한 이 BPR-OPT가 AUROC와 어떤 유사성이 있는지 본다.
BPR-OPT를 발표하는 것에 그치지 않고 효과적으로 최적화할 수 있는 방법인 LEARN-BPR에 대해서도 소개한다. LEARN-BPR을 사용한 BPR-OPT를 기존의 SOTA에 해당하던 모델인 MF와 kNN에도 적용시켰을 때, 그 효과가 얼마나 더 좋은지 나중에 그래프를 통해서 보여준다.
BPR Optimization Criterion
모든 아이템 $i \in I$에 대해서 개인화된 ranking을 찾는 문제는 베이지안 공식에서 사후 확률을 높이는 문제와 같다. 여기서 사후확률 $p(\Theta \vert >_u)$는 $u$의 선호도를 잘 나타낼 수 있는 파라미터 $\Theta$를 잘 찾는 것을 말한다. 하지만 여기서 유저의 선호도 $>_u$는 아직 알지 못하기 때문에 이와 비례하는 사전 확률과 가능도의 곱을 사용해서 학습한다.
$$ p(\Theta \vert >_u) \propto p(>_u \vert \Theta) p(\Theta) $$
유저와 모든 아이템 쌍 $(u, i, j)$에 대해서 학습 데이터와 비교하였을 때, 아래와 같이 2가지의 경우만 나올 수 있는 베르누이 분포가 만족된다. 또한 각각의 유저와 아이템 쌍의 순서에 독립적이기 때문에 모든 유저에 대한 사후 확률을 높이는 것은 각 유저의 곱으로 표현할 수도 있다.
$$
\left\{\begin{matrix}
(u, i, j) \in D_S \\
(u, i, j) \notin D_S
\end{matrix}\right.
$$
각 유저와 아이템 쌍에 대해 독립이고, 베르누이 분포를 따르기 때문에 베르누이 분포의 확률 질량 함수를 이용해 전체 사후 확률을 계산하면 아래와 같다. *참고: 베르누이 분포의 최대 가능도 모수 추정
$$\prod_{u \in U} p(>_u \vert \Theta) = \prod_{(u, i, j) \in U \times I \times I} p(i >_u j \vert \Theta)^{\delta((u, i, j) \in D_S)} \cdot p(1 - p(i >_u j \vert \Theta))^{\delta((u, j, i) \notin D_S)} $$
$$
\delta(b) :=
\begin{cases}
1 &\text{ if } b \text{ is true,} \\
0 &\text{ else}
\end{cases}
$$
위의 수식이 너무 길기 때문에 앞으로 소개할 내용에서는 아래와 같이 줄여서 나타낸다.
$$ \prod_{(u, i, j) \in D_S} p(i >_u j \vert \Theta) $$
바로 위의 수식에서 뒷 항을 계산을 위해서는 $\Theta$를 가지고 유추한 $u$의 $i$에 대한 선호도 $\sigma(\hat{x}_{uij}(\theta))$를 알아야 한다. 정확히는 $u$가 $i$를 $j$보다 선호할 확률에 대해 알고 있어야 한다. 여기서 등장하는 $\sigma$는 값을 0과 1 사이의 값으로 변환해주는 시그모이드 함수를 지칭하며 $\hat{x}_{uij}(\theta)$를 추정할 때는 kNN이나 MF를 사용한다. 이제 이렇게 되면 $u$의 선호도 정보를 반영한 모든 아이템 사이의 ranking을 알 수 있게된다.
지금까지는 $ p(\Theta \vert >_u) \propto p(>_u \vert \Theta) p(\Theta) $에서 likelihood에 대해서 알아봤다면 이제 남은 하나 prior 사전 확률에 대해서 알아봐야 한다. 일반적으로 사전 확률을 계산할 때는 하나의 분포를 따른다고 가정한다. 여기서는 정규분포를 따른다고 가정한다.
$$ p(\Theta) \sim \mathcal{N}(0, \sum_\Theta = \lambda_\Theta I) $$
$$ p(\Theta) \sim \mathcal{N}(0, \lambda_\Theta)= \frac{1}{\sqrt{2\pi \lambda_\Theta}}e^{-\frac{\Theta^2}{2\lambda_\Theta}} \approx e^{-\lambda_\Theta \| \Theta \|^2} $$
사후 확률을 계산하기 위한 준비를 모두 마치었으니, 이제 사전 확률과 가능도의 곱으로 전개하면 된다. 계산의 편리성을 위해서 $\ln$을 취하였으며 BPR-OPT의 전개과정은 아래와 같다.
$$
\begin{align*}
\text{BPR-OPT} :&= \ln p(\Theta \vert >_u) \\
&= \ln p(>_u \vert \Theta) p(\Theta) \\
&= \ln \prod_{(u, i, j) \in D_S} \sigma(\hat{x}_{uij}) p(\Theta) \\
&= \sum_{(u, i, j) \in D_S} \ln \sigma(\hat{x}_{uij}) + \ln p(\Theta)\\
&= \sum_{(u, i, j) \in D_S} \ln \sigma(\hat{x}_{uij}) - \lambda_\Theta \| \Theta) \|^2
\end{align*}
$$
(1) Analogies to AUC optimization
바로 위에서 BPR-OPT에 대한 식을 정의 했다면 왜 AUROC와 유사성을 갖는지 보이는 것은 매우 쉽다. 각 유저별 AUC를 정의하게 되면 다음과 같이 정의한다.
$$ \text{AUC}(u) := \frac{1}{\vert I_u^+\vert \vert I \setminus I_u^+ \vert} \sum_{i \in I_u^+} \sum_{j \in I \setminus I_u^+} \delta (\hat{x}_{uij} > 0) $$
위의 식을 우리가 앞서 정의했던 $D_S$를 사용하여 다시 표현해보면, 아래와 같이 재작성될 수 있다.
$$ \text{AUC}(u) = \sum_{(u, i, j) \in D_S} z_u \times \delta (\hat{x}_{uij} > 0) \quad \text{where, } z_u = \frac{1}{\vert U \vert \vert I_u^+ \vert \vert I \setminus I_u^+ \vert} $$
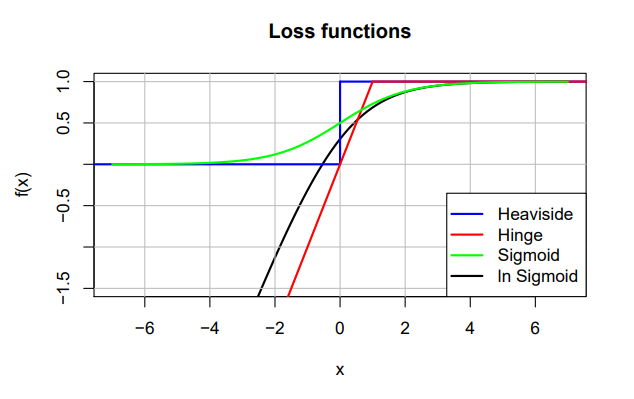
이렇게 보았을 때, AUROC 수식과 우리가 정의했던 BPR-OPT가 매우 유사함을 알 수 있다. 차이점이 있다면 normalizing 해주는 상수 $z_u$에서 차이가 발생한다는 것이다. 또한 AUROC는 미분이 불가능한 $\delta$ 함수를 사용한 것에 반해, BPR-OPT는 미분이 가능한 $\ln \sigma(x)$ 함수를 사용하였다. 정확히는 다른 미분 가능한 함수들도 사용이 가능한데, $\delta$함수를 근사하는 다른 함수들의 종류에는 아래의 사진을 참고할 수 있다.
BPR Learning Algorithm
위의 파트에서는 개인화된 ranking을 계산하는 BPR-OPT에 대해 알아보았다. 이 방법은 미분이 가능하여 경사 하강법을 사용하여 최적화 하는것이 옳게 보일 수 있다. 하지만 아래에서 얘기하겠지만, 경사하강법을 이용한 최적화 방법은 이번에는 좋은 선택이 아니다. 정확한 문제를 지금 짚고 넘어가기보다 이를 해결하기 위한 방법을 먼저 보자면, 저자는 LEARN-BPR이라는 최적화 방법을 소개하였다. 이는 bootstrap 샘플링에 기반을 둔 SGD방식이다. 참고: 부트스트랩 샘플링(Bootstrap Sampling)이란?
LEARN-BPR을 살펴보기 전 다시 경사 하강법에 대해 살펴보자면, 경사 하강법은 크게 모든 데이터를 하나하나 사용하는 Full Gradient Descent와 SGD로 나눌 수 있다. 물론 이 방법은 최적화를 올바르게 해 나가지만, 가장 큰 단점은 수렴 속도가 너무나도 느리다는 것이다. 정확히는 모든 아이템 쌍에 대해서 해야 하기 때문에 $\mathcal{O}(\vert S \vert \vert I \vert)$에 해당하는 시간이 소요된다.
문제는 이뿐만이 아니다. 상호작용한 아이템에 비해 상호작용하지 않은 아이템의 비율이 높기 때문에 $(u, i, j)$를 선택했을 때, $i$가 중복되어서 학습되는 경우가 상당히 많아져 데이터의 불균형이 생기게 되어버린다. 이를 해결하려면 학습률 $\alpha$를 아주 낮게 조정하는 것뿐이다.
일반적인 경사 하강법에 대한 문제를 살펴보았으니, SGD를 적용했을 때는 어떤지도 살펴본다. 위에서 언급했던 것에 비해 데이터의 불균형은 어느 정도 해소가 되었지만, $(u, i, j) \in D_S$를 선택할 때 동일한 $u$와 $i$의 쌍이 너무 많이 학습에 들어간다는 단점이 있다. 그 이유로는 상호작용하지 않은 아이템인 $j$에 해당하는 아이템의 개수가 너무 많기 때문이다.

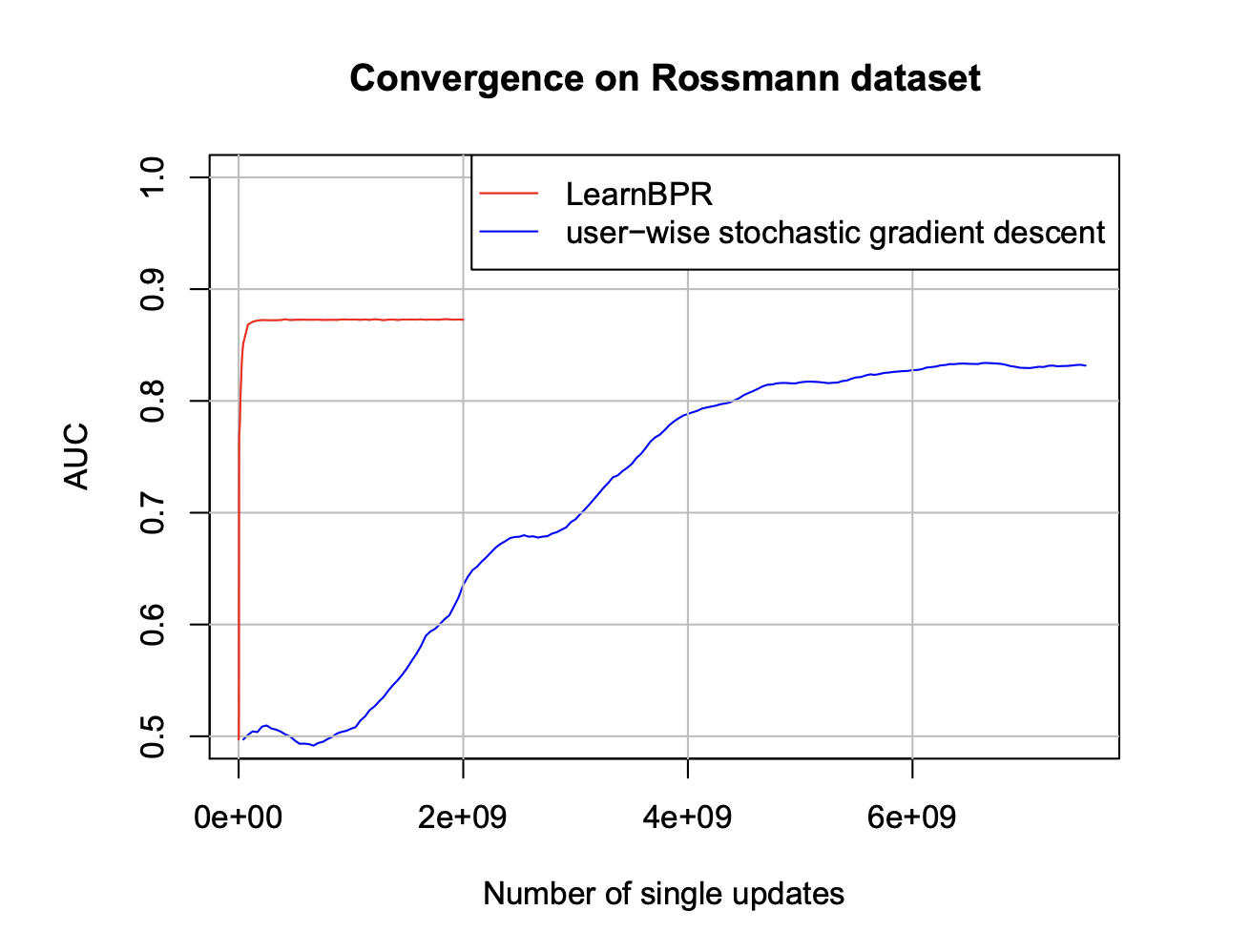
이 문제를 해결하기 위해 저자는 $(u, i, j)$를 하나로 묶어서 triples라고 정의하고 중복된 $u$, $i$쌍이 데이터로 포함되지 않도록 만들었다. 이런 방법을 하기 위해서 bootstrap 기반의 샘플링을 했을 때, 학습 중간에 언제든지 stop 할 수가 있기 때문에 좋다고 하였다. 특히나 이번에 사용하는 데이터는 일반적인 경사 하강법을 적용하기에 수가 너무 많기에 시간이 너무 오래 걸린다는 단점이 있어서 boostrap의 triples 샘플링을 하기에 딱 알맞는다고 주장하였다. 아래의 사진은 학습 횟수에 따른 성능 변화의 그래프이다. 훨씬 더 적은 step에서 이미 높은 성능을 보여주는 것을 바로 확인할 수 있다.
Learning models with BPR
이번 파트에서는 LEARN-BPR 방법을 다른 모델들에도 적용시켰을 때 어떤 성능을 보이는지 실험을 통해 보인다. 적용한 모델은 MF기반의 모델 2개와 kNN모델이다. 이 모델들은 전부 예측값으로 유저 $u$의 아이템 $l$에 대한 선호도 $\hat{x}_{ul}$를 사용한다. 따라서 LEARN-BPR은 $(u, i, j)$를 사용하기 때문에 다음과 같이 바꿔준다.
$$ \hat{x}_{uij} := \hat{x}_{ui} - \hat{x}_{uj} $$
(1) Matrix Factorization
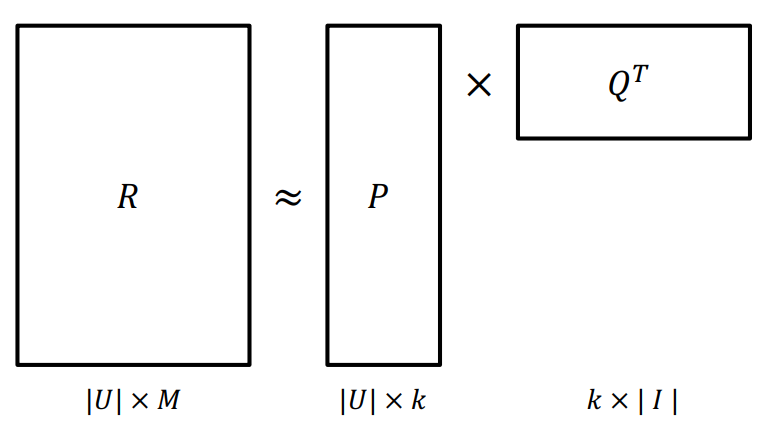
MF는 $\hat{x}_{ui}$를 예측하도록 설계되었는데 이는 사실 유저-아이템 행렬 $X$를 추정하는 것과 같다. MF는 이 행렬을 추정하기 위해서 유저 행렬과 아이템 행렬 2개로 분해해서 학습하도록 한다.
$$ \hat{X} := WH^T $$
- $W$ : 유저 잠재 행렬 $\vert U \vert \times k$
- $H$ : 아이템 잠재 행렬 $\vert I \vert \times k$
- $k$ : 잠재 행렬의 차원 (number of latent factors)
MF에서는 $\hat{x}_{ui}$를 계산하기 위해서 유저 잠재 벡터 $w_u$와 아이템 잠재 벡터 $h_i$를 사용하여 유사성을 판단한다. 유사성을 계산하기 위해서 2개의 벡터를 내적하여 다음과 같이 계산한다.
$$ \hat{x}_{ui} = \left \langle w_u, h_i \right \rangle = \sum_{f=1}^k w_{uf} \cdot h_{if} $$
위와 같이 $\hat{X}$를 $X$에 근사 시키기 위해서는 SVD를 사용한 최소 제곱합을 이용해 학습하는데, 문제는 SVD가 과적합이 너무 쉽게 일어난다는 것이다. 따라서 많은 MF방법들은 regularization term을 추가해서 과적합을 피하도록 만들었다. ranking을 사용하여 학습을 하기 위해서는 앞서 소개한 LEARN-BPR을 사용한다. 이때, $\hat{x}_{uij}$에서 사용될 파라미터인 $w_{uf}, h_{if}, h_{jf}$에 대해 미분 값을 구해줘야 한다. 여기에 과적합을 피하기 위해 저자들은 3가지 regularization term을 사용하였으며, 각각 유저에 대한 규제 $\lambda_W$와 상호작용한 아이템에 대한 규제 $\lambda_{H^+}$와 상호작용하지 않은 아이템에 대한 규제 $\lambda_{H^-}$이다.
(2) Adaptive k-Nearest-Neighbor
협업 필터링에서 이웃 기반 방식은 굉장히 인기 있는 방법이다. 유저와 아이템 간의 유사도를 비교하여 아이템을 추천해주는 방식이다. 이웃 기반은 유저 기반과 아이템 기반이 있는데, 일반적으로 아이템 기반의 방법이 유저 기반보다 더 좋은 성능을 보여준다. kNN은 가장 유사한 $k$개의 아이템들을 보고 예측하는 방법을 말한다. 더 정확히 수식을 보면 아래와 같다.
$$ \hat{x}_{ui} = \sum_{l \in I_u^+ \wedge l \neq i} c_{il} $$
- $C$ : 아이템-아이템 행렬, $I \times I$
일반적으로 $C$를 학습하거나 계산하는 방법은 유사도 함수를 사용해서 채워 넣는 것이다. 유사도 함수는 휴리스틱 하게 선택하며 대표적으로 코사인 유사도나 Jaccard 유사도를 사용한다. 사실 이 보다 더 좋은 방식은 $C$를 학습 파라미터로 설정하여 스스로 학습하게 만드는 것이다. 만약 $C$의 크기가 너무 크다면 $H : I \times k$ 행렬 2개로 쪼개서 학습시킬 수 있다. MF와 마찬가지로 이를 학습시키기 위해서 BPR-OPT와 LEARN-BPR을 적용시켜서 학습할 수 있다. 각 파라미터에 대한 그래디언트는 아래와 같다.
$$
\frac{\partial}{\partial \theta} \hat{x}_{uij} =
\begin{cases}
+1 & \text{if } \theta \in \{ c_{il}, c_{li}\} \wedge l \in I_u^+ \wedge l \neq i \\
-1 & \text{if } \theta \in \{ c_{jl}, c_{lj}\} \wedge l \in I_u^+ \wedge l \neq j \\
0 & \text{else}
\end{cases}
$$
학습할 때는 과적합을 피하기 위해 2개의 regularization term을 사용하고, 각각 $\lambda_+$와 $\lambda_-$이다.
EVALUATION
평가에서는 다른 학습 방법과 BPR을 사용했을 때를 비교하여 보여준다. 비교대상으로는 MF에 기반을 둔 주요 모델 2개와 kNN을 선택하였다.
Datasets

저자들은 2개의 다른 데이터셋을 사용하였다. 하나는 온라인 쇼핑몰 데이터셋인 Rossman이었으며 이는 10,000명의 유저와 4,000개의 아이템 사이의 상호작용 정보를 가지고 있다. 상호작용의 개수는 총 426,612 개이다. 두 번째 데이터셋은 DVD 렌털 업체인 Netflix 데이터셋이며, 유저들이 각 영화에 1~5점 사이의 어떤 평점을 남겼는지 적혀이다. 특히 이번 논문의 경우 Explicit Feedback이 아닌 Implicit Feedback데이터를 사용하길 원했으므로 평점이 있는 모든 데이터들을 1로 변경하였다. 넷플릭스 데이터는 10,000명의 유저와 5,000개의 아이템 사이의 상호작용 정보를 가지고 있으며 총 개수는 565,738개에 달했다.
Evaluation Methodology

이번에는 평가를 위한 세팅에 대해서 설명한다. 먼저 데이터를 train과 test로 분리하고 유저마다 상호작용에서 1개의 데이터를 제거한다. (leave one out) 그리고 학습할 때, 제거된 데이터를 맞추도록 하는 것이다. 평가는 AUC정보를 사용했으며 더 높은 결괏값이 더 좋은 성능을 보인다. 일반적으로 AUC는 0.5가 가장 기본 성능, 1이 최대 성능을 말한다. 이 학습을 총 10번 했으며, 각 학습마다 데이터를 제거하는 아이템을 새롭게 정하였다. 하이퍼 파라미터 탐색은 grid search로 하였으며, 첫 번째 학습단계에만 적용하고 나머지 9번의 학습에서는 하이퍼 파라미터를 고정시켰다.
Results and Discussion
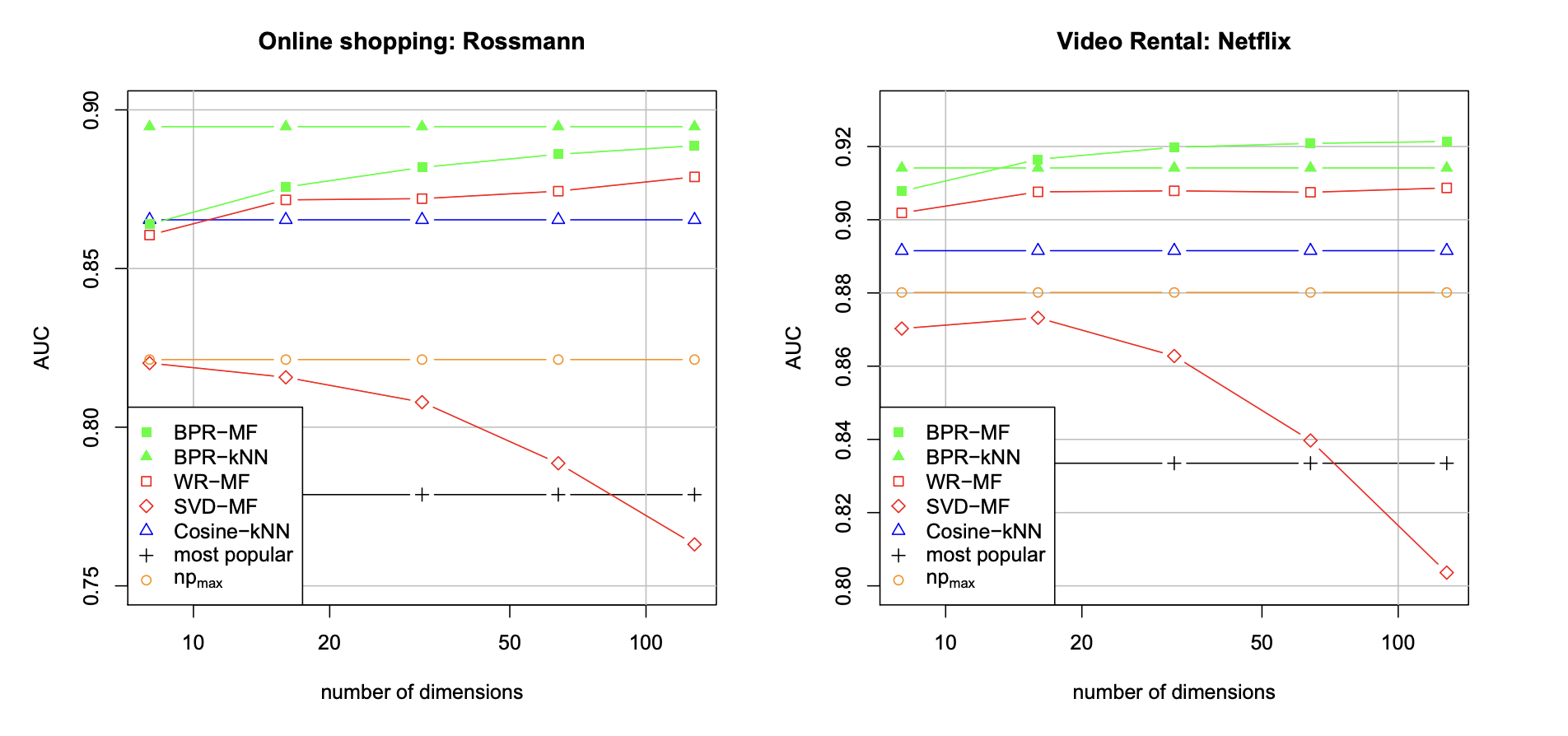
위의 실험 결과를 보았을 때 가장 먼저 눈에 띄는 것은 BPR을 적용시킨 것이 두 데이터셋에서 모두 좋은 성능을 보였다는 것이다. 같은 Matrix Factorization 모델이어도 학습 방법에 따라 성능 차이가 많이 존재했으며, SVD의 경우 차원이 증가할수록 성능이 크게 감소함을 보였다.
요약하자면, 모델의 파라미터를 적절한 최적화 방법과 기준으로 학습하는 것이 중요하다는 것을 보였다. 실험적인 결과로 LEARN-BPR로 학습한 BPR-OPT가 다른 SOTA에 비해서 Implicit Feedback에 대해 뛰어난 성능을 보여주었다. 따라서 유저의 선호도를 반영한 아이템 ranking 문제에 있어서 BPR(BPR-OPT + LEARN-BPR)을 사용하여 학습하는 것이 좋다고 밝힌다.




