| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | |||||
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| 17 | 18 | 19 | 20 | 21 | 22 | 23 |
| 24 | 25 | 26 | 27 | 28 | 29 | 30 |
- CF
- SGNS
- Skip-gram
- Ai
- TTS
- Noise Contrastive Estimation
- Tacotron2
- 논문리뷰
- Item2Vec
- Recommender System
- 부스트캠프 AI Tech
- wavenet
- FastSpeech
- Dilated convolution
- 추천시스템
- RecSys
- FastSpeech2
- CV
- ALS
- matrix factorization
- BOJ
- NEG
- Implicit feedback
- Negative Sampling
- Collaborative Filtering
- Neural Collaborative Filtering
- Tacotron
- word2vec
- 백준
- ANNOY
- Today
- Total
devmoon
Neighborhood Based Collaborative Filtering (UBCF, IBCF) 본문
협업 필터링 방식은 다른 사람들의 데이터를 바탕으로 나의 추천을 결정하는 방법론을 말한다. 기본적으로 다른 유저의 데이터가 많이 존재할수록 추천 성능이 올라갈 것이라는 믿음을 바탕으로 생겨났으며 이번 글은 다양한 협업 필터링 중 최초로 등장한 이웃 기반 협업 필터링(Neighborhood Based Collaborative Filtering)에 대해 다룬다.

예를 들어, A와 B가 온라인 쇼핑몰에서 상품을 구매하고자 할 때 전자제품들을 많이 구매했다면, A가 다음으로 좋아할 만한 상품들을 B의 기록을 통해서 추천하는 것이다. 둘이 동일한 성향을 가지고 있는데 B가 특정 상품에 대해 안 좋은 평가를 내렸다면, A도 그 상품을 좋아하지 않을 확률이 크기 때문이다. 지금과 같은 예시는 유저를 기반으로 한 협업 필터링이며, 반대로 평점을 비슷하게 받은 아이템들을 기반으로 협업 필터링을 하는 것도 가능하다.
Neighborhood Based Collaborative Filtering
User Based Collaborative Filtering

4명의 사람이 5개의 영화에 내린 평점 정보가 있고, B가 스타워즈에 내릴 평점을 예측하고 싶다고 할 때 협업 필터링을 사용할 수 있다. 유저 기반 협업 필터링은 나와 유사한 유저를 찾아 그 사람의 평점 정보를 나의 평점 정보 예측에 사용하는 것이다. 위에서는 User A가 User B와 다른 작품에 대해 대체로 비슷한 평점을 내려서 유사하다고 생각해 볼 수 있다. 그렇기에 "스타워즈에도 User B는 높은 평점을 내릴 것이다"라고 예측이 가능하다.
Item Based Collaborative Filtering

아이템 기반 협업 필터링은 현재 아이템과 가장 비슷하게 평점이 내려진 아이템을 찾아 추천에 사용하는 방법이다. 위의 예시에서는 user A와 user B의 스타워즈 평점이 헐크나 아이언맨과 유사하게 매겨진 것을 볼 수 있다. 상위 2명의 유저들은 비교적 높은 평점들을 주었지만 User C, D는 대체로 낮은 평점을 주었다. 여기서 우리는 User B가 스타워즈에 내릴 평점도 유사한 사람들의 평점 정보를 사용해 약 4~5점을 매기겠다고 예측할 수 있다.
KNN Collaborative Filtering
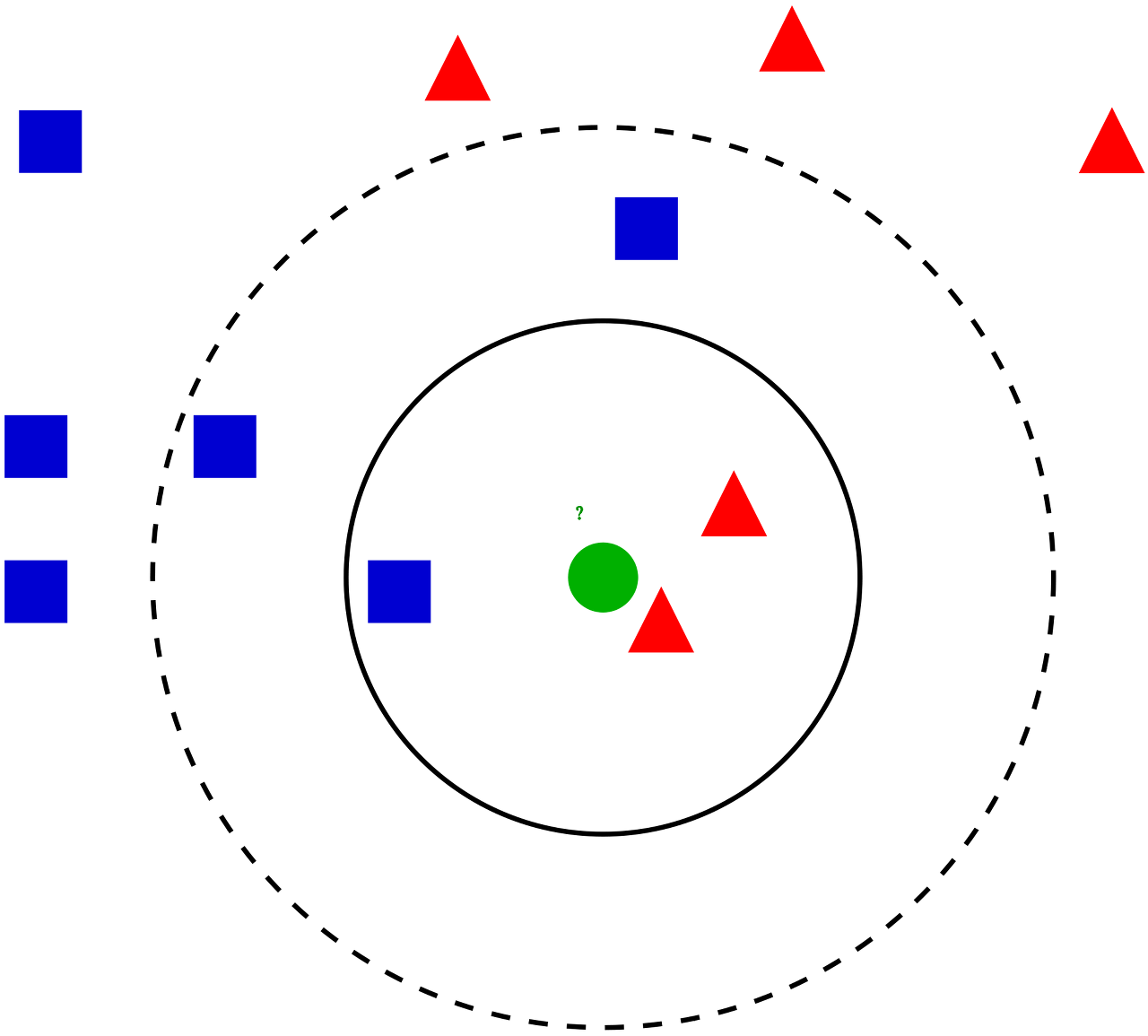
이웃 기반 협업 필터링의 한계에는 다른 유저들과의 유사도를 모두 구하고 계산에 사용해야 한다는 점이 있다. 유저가 많아지면 많아질수록 유사도를 구하는데 더 많은 시간이 걸리게 될 것이며, 오히려 성능이 떨어트리기도 한다. 이에 등장한 KNN 협업 필터링은 현재 유저와 가장 유사한 $K$명의 유저를 사용해 평점 정보를 예측하게 된다. 일반적으로 $K$는 25~50 사이의 값을 사용하지만 상황에 따라 여러 가지 실험을 통해 직접 설정해야 하는 값이다.
Similarity Function
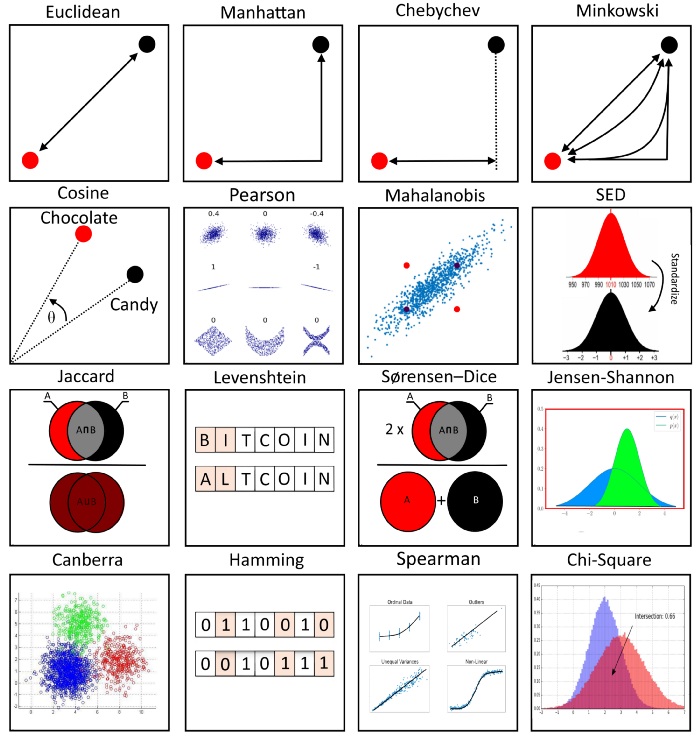
협업 필터링에서는 계속 아이템 또는 유저를 기반으로 유사한 다른 아이템, 유저를 찾아 평점 예측을 진행했었다. 따라서 두 유저 또는 두 아이템 사이의 유사도를 측정하는 방법이 필요하다. 실제로 유사도를 측정하는 방법에는 여러 가지가 있지만, 추천 시스템에서 자주 사용되는 Cosine유사도, Jaccard유사도를 포함한 4가지 함수에 대해서만 알아보고자 한다.
Mean Squared Difference Similarity
MSDS 함수는 두 유저가 내린 평점 간의 차이를 계산하여 그 차이가 작을수록 더 많이 유사하다고 판단하는 함수이다. 동일한 아이템에 내린 두 유저의 평점 차를 제곱하여 더한 후, 더한 개수만큼 나누어 평균을 구하는 방식이다. 유사도는 이 결괏값과 역수 관계를 가지고 있기 때문에 마지막에 역수를 취해준다.
$$ \text{MSD}(u, v) = \frac{1}{\vert I_{uv} \vert} \sum_{i \in I_{uv}} (r_{ui} - r_{vi})^2 $$
$$ \text{MSDS}(u, v) = \frac{1}{\text{MSD}(u, v) + 1} $$
- $u, v$ : 2명의 유저를 지칭
- $I_{uv}$ : 유저$u$와 유저$v$가 모두 평점을 내린 아이템 집합
Cosine Similarity

위의 MSDS에서는 평점 차이 정보를 사용했다면, 코사인 유사도는 유저의 평점 정보들을 벡터 공간에 매핑시켰을 때, 두 벡터가 얼마나 비슷한 곳을 가리키고 있는지 계산한다. 벡터 공간에서 벡터는 각 유저를 말하며 코사인 유사도의 결과가 1에 가까울수록 많이 유사함을 의미하고, -1에 가까울수록 두 유저는 정반대의 성향을 가졌다고 해석한다.
$$ \cos(\theta) = \cos(X, Y) = \frac{X \cdot Y}{\vert X \vert \vert Y \vert} = \frac{\sum_{i=1}^N X_iY_i}{\sqrt{\sum_{i=1}^NX_i^2}\sqrt{\sum_{i=1}^NY_i^2}} $$
Pearson Similarity
피어슨 유사도는 피어슨 상관계수를 사용한 유사도로, 코사인 유사도와 그 수식이 유사하다. 차이점은 각 벡터의 값을 벡터의 표본 평균값으로 정규화해주었다는 것이다. 따라서 주로 낮게 평점을 매기는 사람과 주로 높게 평점을 매기는 사람과의 차이를 보정해줄 수 있다. 코사인 유사도와 마찬가지로 1에 가까울수록 더 유사한 관계를 갖는다는 것을 의미한다.
$$ \text{pearson sim}(X, Y)=\frac{\sum_{i=1}^{N}(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{\sum_{i=1}^{N}(X_i-\overline{X})^2}\sqrt{\sum_{i=1}^{N}(Y_i-\overline{Y})^2}} $$
Jaccard Similarity
Jaccard 유사도는 벡터가 아닌 집합을 사용한 유사도로 꽤나 개념이 단순하다. 두 유저가 소비한 전체 아이템 중, 둘 다 소비한 아이템이 개수의 비율을 유사도로 사용한다. 이론적으로 벡터가 아니기 때문에 두 유저의 차원이 달라도 유사도를 계산하는 것이 가능하다. 두 유저가 소비한 아이템이 완전히 동일하다면 결괏값은 1이 되며 겹치는 아이템이 존재하지 않는다면 결과는 0이 된다.
$$ \text{Jaccard}(A,B)=\frac{|A\cap B|}{|A\cup B|}=\frac{|A\cap B|}{|A|+|B|-|A\cap B|} $$
Jaccard 유사도를 평점 정보에 사용하고 싶을 때는, 평점을 매긴 아이템 중 4점을 넘긴 아이템만을 뽑아서 유사도를 계산해도 된다. 그럴 경우, 전체 아이템 중 동일한 아이템에 높은 평점을 매긴 아이템의 비율을 구할 수 있어서 평점 정보를 예측하는 데 사용할 수 있다.
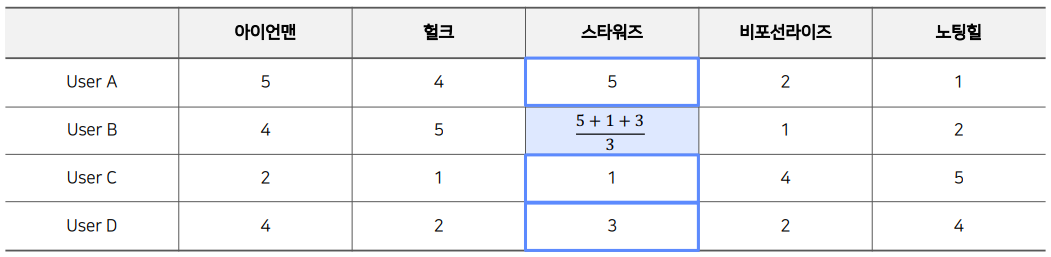
이제 실제로 평점 예측을 진행하는데, 위와 같이 다른 사람들의 평점 정보들을 사용하여 평균을 가져오게 된다면 당연히 적절하지 못하다고 생각이 든다. 특히 User C의 경우 User B와 성향이 완전 다른데, 그 정보를 그대로 가져와서 쓰는 것이 형평성에 맞지 않는 것이다. 따라서, 위에서 살펴보았던 유사도 정보를 가중치로 사용하여 평점에 반영하도록 계산해볼 수 있다.
$$ \frac{\sum_u sim(u_B, u) \cdot r_{ui}}{\sum_u sim(u_B, u)} $$
- $sim(u_B, u)$ : user B와 $u$ 의 유사도
하지만, 이렇게 유사도를 가중치로 활용을 하더라도 문제점이 있다. 어떤 사람은 대체로 평점을 짜게 주는 편이라서 3점을 준 것이 매우 높게 평점을 매겼을 수 있고 반대로 어떤 사람은 평점을 높게 주는 편이라서 3점을 준 것이 매우 낮게 평점을 준 것일 수도 있다. 이렇게 각 유저마다 평점을 주는 편향이 생길 수 있어서 유저가 매긴 점수에서 그 평균을 뺀 편차 정보를 사용하여 평점 예측을 해보는 방법을 떠올려볼 수 있다. 이 방법을 Relative Rating이라고 부른다.
$$ \hat{r}_{ui} = \bar{r_u} + \frac{\sum_{u' \in \Omega_i} sim(u, u') \cdot (r_{u'i} - \bar{r_{u'}})}{\sum_{u' \in \Omega_i} sim(u, u')} $$
- $\hat{r}_{ui}$ : $u$가 $i$에게 매길 평점 예측값
- $\bar{r_u}$ : $u$가 매긴 평점들의 평균
- $\Omega_i$ : $i$에 평점을 내린 유저들의 집합
마찬가지로 IBCF도 똑같이 진행하면 된다. 그 기준이 행이 되는지 열이 되는지가 차이일 뿐이며 수식에서는 기호 몇 개가 변경되는 것이 다이다.
$$ \hat{r}_{ui} = \bar{r_i} + \frac{\sum_{i' \in \Phi_u} sim(i, i') \cdot (r_{ui'} - \bar{r_{i'}})}{\sum_{i' \in \Phi_u} sim(i, i')} $$
- $\Phi_u$ : $u$가 평가한 아이템들의 집합
이웃기반 협업 필터링을 소개하면서 등장한 예시들에서는 대부분의 평점 정보가 채워져 있었다. 하지만 실제 데이터에서는 대부분의 칸이 비어져있다. 생각해보면 실제로 평점을 잘 매기지 않는 사람이 대부분 이기에 당연하기도 하다. 전체 칸 대비 비워져 있는 칸의 비율을 sparsity ratio라고 하며, 그 비율이 99.5% 이상이라면 사실상 이웃 기반 협업 필터링을 사용하기에는 무리가 있다. 이후에 모델 기반 협업 필터링인 Matrix Factorization이라는 방법을 사용해 이 단점을 보완하는 것이 가능하다.
'AI > 추천 시스템' 카테고리의 다른 글
| ANN: Approximate Nearest Neighbor (0) | 2023.01.03 |
|---|---|
| Content Based Recommendation / TF-IDF (0) | 2022.11.02 |
| 연관 규칙 탐색 알고리즘 (2) | 2022.10.24 |
| 연관 규칙 분석 / support, confidence, lift (0) | 2022.10.22 |
| 인기도 기반 추천 (조회 / 평점) (0) | 2022.10.20 |




