| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Implicit feedback
- TTS
- Skip-gram
- 백준
- CF
- wavenet
- word2vec
- Dilated convolution
- BOJ
- 부스트캠프 AI Tech
- Ai
- NEG
- SGNS
- RecSys
- Tacotron2
- Neural Collaborative Filtering
- Negative Sampling
- FastSpeech2
- Recommender System
- matrix factorization
- ALS
- Tacotron
- ANNOY
- 논문리뷰
- Item2Vec
- Noise Contrastive Estimation
- 추천시스템
- CV
- Collaborative Filtering
- FastSpeech
- Today
- Total
devmoon
[논문 리뷰] Batch Normalization 본문
딥러닝을 공부하고 모델링을 진행하다 보면 자주 등장하는 개념이 Batch Normalization이다. 번역해서 배치 정규화라고도 불리는데, 대략적인 개념을 알지만 그 세세한 작동원리와 그 구조를 자세하게 알고 싶어서 리뷰할 논문으로 선택하였다. 배치 정규화를 사용했을 때, 14배 빠른 속도로 동일한 성능을 보일 수 있다니 대단한 개념이라고 생각되었다.
배치 정규화를 가장 처음에 요약하고 시작하자면, 딥러닝 구조의 각 레이어에서 입력들의 분포가 항상 유사하거나 일정하도록 만들어주는 것이다. 입력 분포가 일정하지 않으면 무엇이 문제이고 어떤 단점들이 있는지 논문에서 잘 설명해주어서 그 중요성을 많이 깨닫게 되었다.
Introduction
처음에 논문은 SGD의 장점들에 대해서 설명한다. SGD는 딥러닝 모델을 학습하는데 있어 매우 효과적인 성능을 보여주고 있으며, 특히 미니 배치를 사용한 SGD는 배치 사이즈가 클수록 전체 데이터를 추정하는 것이 더 정교해진다. 또한 현대 컴퓨터가 발전함에 따라 미니 배치를 사용하면 더 빠른 속도로 연산을 진행할 수 있다는 장점도 존재한다.
이렇게 좋아보이는 SGD도 단점이 있는데, 모델에 사용되는 하이퍼파라미터를 초기화할 때 주의를 기울여야 하는 것이었다. 또한 이전 레이어의 출력이 다음 레이어에 계속 영향을 주는 딥러닝 네트워크의 특성상 작은 변화가 레이어를 점점 더 많이 거칠수록 큰 변화가 될 수 있다는 문제점이 있다.

레이어에 들어가는 입력의 분포가 바뀌게 되면 모델의 파라미터들은 새로운 분포에 대해서 다시 적응하고 학습하는 과정을 거쳐야만 했다. 그리고 이런 train과 test 데이터의 입력분포의 차이를 covariate shift 라고 부르게 된다. 따라서 입력의 분포를 고정시키는 것이 학습을 더 원활하게 할 수 있게 한다. (모델의 파라미터들이 새로운 분포에 적응할 필요X)
논문의 저자는 예로 간단한 1층 레이어의 딥러닝 구조를 가져왔다. 간단한 affine transformation ($Ax + b$ 꼴)에 시그모이드 함수를 사용하여 아래와 같은 수식을 띤다.
$$ z = g(Wu + b) $$
- $g$ : 시그모이드 함수
- $u$ : 입력 데이터

위에서 $Wu + b$ 의 값을 $x$라고 한다면, 이 $\vert x \vert$ 의 값이 커질수록 그때의 그래디언트 값은 0에 가까워지게 된다. 다시 말해, $\vert x \vert$ 가 작지 않다면 모델의 학습 속도는 느려지고 기울기가 소실되는 문제점이 생긴다는 것이다.
하지만 위의 문제는 단순히 활성 함수인 $g(x)$ 를 시그모이드나 하이퍼볼릭 탄젠트 함수가 아닌 ReLU를 사용하고 파라미터의 초기화를 잘하고 학습률을 낮게 설정해서 문제를 해결할 수 있었다. 근데 만약 여기서 활성 함수에 들어가는 입력의 분포가 좀 더 안정화될 수 있다면 그래디언트가 0인 지점(saturated regime)에 빠질 일이 줄어들기 때문에 학습이 가속될 수 있다.
앞서 설명한 레이어를 거듭할수록 생기는 입력 분포의 차이를 저자들은 Internal Covariate Shift라고 칭하는데 앞으로 자주 등장하게 될 용어이다. 결국 이 Internal Covariate Shift 문제를 해결해야 원활한 학습이 이루어질 수 있음을 보이는 것이 궁극적인 목표이다. 또한 Interncal Covariate Shift를 해결할 수 있는 방법이 이번 논문의 제목인 Batch Normalization이라고 밝히며 본격적으로 소개하기 전 그 장점들을 나열한다.
- 높은 학습률을 설정할 수 있다.
- 모델에 규제를 걸 수 있다.
- Dropout의 효과를 낼 수 있다.
- 양의 무한대 또는 음의 무한대의 미분 값이 0에 수렴하는 Saturating 활성 함수를 사용할 수 있게 한다.
Towards Reducing Internal Covariate Shift
2번째 파트에서는 Internal Covariate Shift를 줄이기 위해 시도한 여러 가지 방법과 그 문제점들에 대해서 소개한다. 주 해결점은 각 레이어의 입력에 대한 분포를 고정시키는 것이다. 저자들은 처음으로 데이터들의 분포를 평균을 0, 분산이 1이게 만들고 decorrelation 시키는 whitening 기법을 적용시켜보았다.
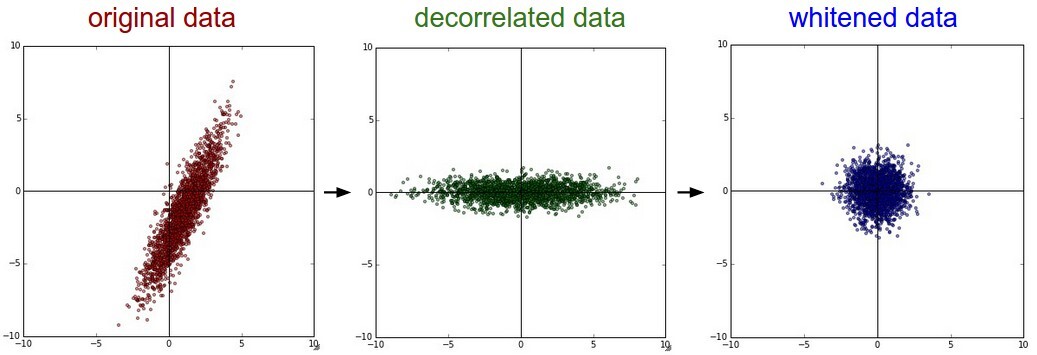
위의 whitening 기법의 결과물을 보면 항상 데이터가 특정 분포를 따르도록 강제할 수가 있다. 이렇게 되면 Internal Covariate Shift를 제거하는 것이 가능하다. 하지만 문제점은 whitening 기법을 모델에 적용시킬 때 발생한다. 어쨌든 모델의 구조를 직접 수정하거나 파라미터를 수정하여 whitening 기법을 적용시켜야 하는데 이렇게 되면 경사하강법을 통한 오차역전파가 제대로 이루어지지 않게 된다는 문제점이 있다.
논문에서는 왜 경사하강법이 제대로 동작하지 않는지 하나의 예시를 들면서 설명한다. 입력 데이터에 대해서 전체 데이터들의 평균을 빼주고 표준편차로 나누어 정규화를 하는 간단한 예시이다.
$$ \hat{x} = x - \mathbb{E}[x] \quad \text{where, } \mathbb{E}[x] = \frac{1}{N} \sum_{i=1}^{N} x_i $$
$$ x = u + b \qquad \mathcal{X} = \{ x_{1\dots N} \} $$
위에서 $N$은 전체 데이터의 수를 말하며 $\mathbb{E}[x]$는 전체 데이터의 평균을 의미한다. $b$ 의 값은 $b \leftarrow b + \Delta b$ 와 같이 업데이트되고 업데이트된 $b$ 를 다시 다음 레이어에 전달하게 되면 아래와 같이 표현할 수 있다.
$$ u + (b + \Delta b) - \mathbb{E}[u + (b + \Delta b)] = u + b - \mathbb{E}[u + b] $$
위의 결과를 통해 알 수 있는 것은, 아무리 파라미터 $b$가 업데이트된다고 하더라도 정규화시킨 레이어의 출력은 이전과 같다는 것이다(경사하강법에서 정규화 과정에 대한 역전파가 무시되는 효과). 또한, 업데이트 되는 파라미터 $b$의 값은 그래디언트가 계속 더해져 무한으로 커지게 되는 반면 loss 값은 값을 유지한다.
그러면 이제 다시 위의 문제(역전파에서 정규화 과정이 생략되는 문제)를 해결해서 어떤 파라미터를 사용하더라도 네트워크의 출력들이 항상 고안된 분포를 따르도록 보장해주어야 한다. 다시 $x$를 레이어의 입력 벡터, $\mathcal{X}$ 를 전체 데이터셋에서 등장하는 모든 입력 벡터라고 한다면 정규화를 아래와 같이 묶어서 표현해볼 수 있다.
$$ \hat{x} = \text{Norm} (x, \mathcal{X}) $$
위의 수식은 현재 입력 벡터 $x$ 뿐만 아니라, 전체 학습 데이터의 입력 벡터 $\mathcal{X}$에도 정규화 과정에 포함되어있다. 이제 마찬가지로 역전파 과정을 살펴보아야 하는데 $\text{Norm}$ 은 다변수 함수이기 때문에 Jacobians 행렬을 계산해야만 한다.
이렇게 되면 레이어의 입력에 대해 Whitening을 하는 것이 새로운 공분산 행렬과 inverse square root를 구해서 미분해야 하기 때문에 연산량이 많아져 비효율적이라고 한다. 그렇기에 저자들은 다음 조건들을 만족하는 새로운 방법을 찾아야 했다.
- 그래디언트를 계산해야 하기 때문에 미분이 가능한 연산이어야 한다.
- 파라미터를 업데이트할 때마다 전체 데이터에 대한 연산을 요구하지 않아야 한다.
Normalization via Mini-Batch Statistics
각 레이어에 대해서 whitening 과정을 거치는 것에 대한 cost가 높고 모든 곳에서 미분이 불가능했기 때문에, 저자는 2가지 간소화 과정을 거친다. 첫 번째는 입력 데이터의 각 스칼라 값인 차원에 대해서 독립적으로 정규화시키는 것이다. 아래에서 구하는 평균과 분산 값은 전체 학습 데이터에서 사용되는 입력의 각 차원에 대해 계산된 값을 의미한다.
$$ \hat{x}^{(k)} = \frac{x^{(k)} - \mathbb{E}[x^{(k)}]}{\sqrt{\text{Var} [x^{(k)}]}} $$
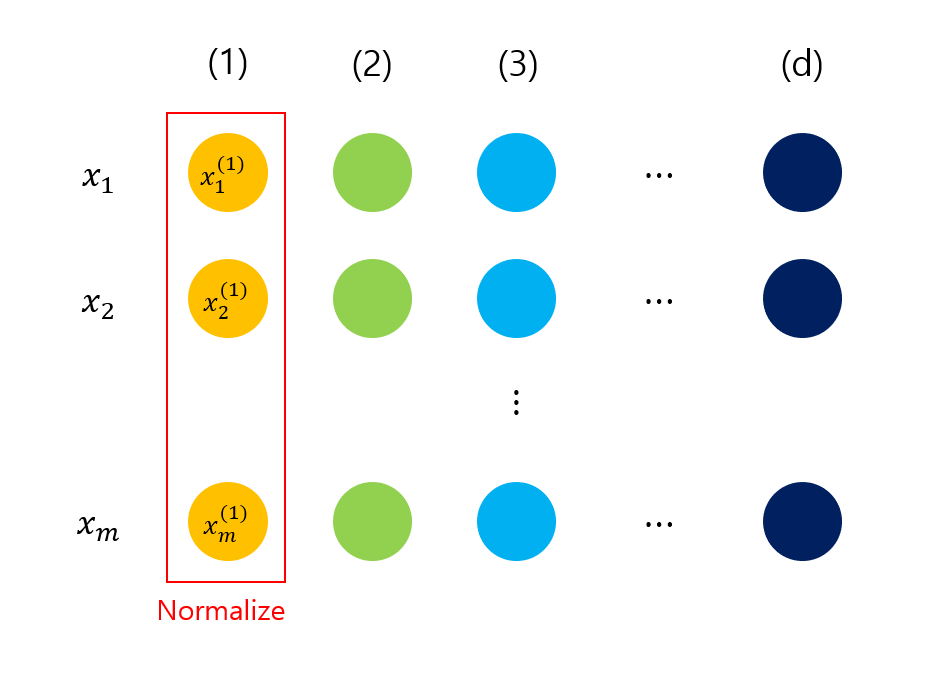
현재까지만 보았을 때, 정규화를 통해 각 차원의 스칼라 값이 평균이 0이고 표준편차가 1인 분포를 따르게 되었다. 이제 이 값들이 시그모이드 활성 함수를 거쳐 다음 레이어로 전달된다고 하면 문제가 생길 수 있다. 문제를 생기기 전에 시그모이드함수의 생김새를 다시 살펴보아야 한다.
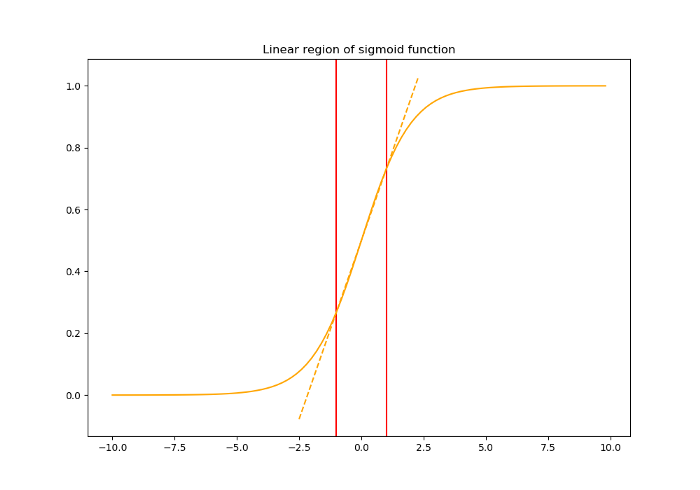
시그모이드 함수의 구간 [-1, 1]을 살펴보면 거의 linear 한 부분이기 때문에, 활성 함수의 특징인 비선형성을 가져갈 수가 없게 된다. 이렇게 되면 딥러닝의 본질인 레이어를 많이 쌓는 이점을 전혀 가져갈 수가 없게 된다. 따라서 이문제를 해결하기 위해 정규화된 값들을 이동시켜주거나 정규화 이전의 값을 전달하도록 해야 한다. 저자는 각 정규화를 진행하는 각 차원마다 새로운 2개의 파라미터인 $\gamma^{(k)}$ 와 $\beta^{(k)}$ 도입하며 문제를 해결한다. (Scalining과 Shifting)
$$ y^{(k)} = \gamma^{(k)} \hat{x}^{(k)} + \beta^{(k)} $$
필요에 따라서는 $\gamma^{(k)} = \sqrt{\text{Var} [x^{(k)}]}$ 로 설정하고, $\beta^{(k)} = \mathbb{E}[x^{(k)}]$ 로 설정함으로써 원래의 출력으로도 복원시킬 수 있게 만들 수 있다. 주목적은 정규화된 값에 scaling과 shifting을 하는 것이다.
배치를 사용한 학습에서는 전체 데이터에 대한 평균과 분산 값을 구하는 것이 불가능하다. 따라서 배치에 대한 평균과 분산값을 통해 정규화를 진행해야 하며 이때 생성된 배치마다의 평균과 분산은 전체 데이터에 대한 모평균과 모 분산을 추정하게 된다. 바로 이것이 두 번째 간소화 과정이다. 지금까지 소개한 개념이 Training 과정에서의 배치 정규화의 전부이다.

이후에 논문은 역전파를 통해 loss 가 전달되는 수식을 설명하며 전체 구간에 대해서 미분이 가능함을 보인다. 또한 정규화 과정이 정상적으로 진행됨에 따라 input에 대한 분포를 일정하게 유지할 수 있어 internal covariate shift 문제를 해결하고, 학습 속도를 향상할 수 있다고 하였다.
Training and Inference with Batch-Normalized Networks
이제까지 Training 과정에 대한 배치정규화를 알아보았다면 마찬가지로 Inference 과정에 대한 배치정규화도 알아보아야 한다. 하지만 생각해보면 Inference 과정에서는 그 입력 단위가 배치가 아닌 한 개의 입력 데이터이므로 평균과 분산 값을 어떻게 설정해야 하는지 고민해야 하는 문제가 생긴다.
따라서 저자들은 Training 과정에서 사용한 배치들의 평균인 표본 평균들을 사용해 모평균을 근사하여 사용하도록 하였다. 분산도 마찬가지이다. 따라서 Test(Inference) 과정에서 사용하는 평균과 분산 값은 값이 고정되어 있으므로 정규화 과정이 사실상 하나의 선형 변환 수식을 추가한 것과 마찬가지이다.
$$ \mathbb{E}[x] = \mathbb{E}_\mathcal{B}[\mu_\mathcal{B}] $$
$$ \text{Var}[x] = \frac{m}{m - 1} \mathbb{E}_\mathcal{B}[\sigma^2_\mathcal{B}] $$
기존의 딥러닝 구조에서는 높은 학습률을 사용하게 되면 그래디언트 값이 0에 가까워져 학습이 이루어지지 않는 문제가 있었다. 하지만, 배치정규화와 함께라면 활성 함수에서 너무 끝쪽으로 이동하지 않고 중앙 부근으로 입력 분포를 바꾸어주기 때문에 높은 학습률을 설정하더라도 괜찮다.
배치를 사용한 학습에서는 어떠한 학습 샘플이 다른 예제들과 함께 묶여서 등장하기 때문에, 특정 입력에 맞게 출력을 내보내는 결정론적인 모델이 되지 않도록 방지할 수 있다. 이 장점은 전체 모델을 regularize 하는데 좋으며 배치정규화는 Dropout처럼 특정 노드에 대한 activation을 제거하거나 감소시키는 효과를 낼 수도 있다고 한다.
이후 논문은 여러 가지 실험을 통해 배치정규화를 통해 학습을 했을 때, 14배 빠른 속도로 비슷하거나 더 높은 성능을 끌어내는 것을 관찰했다고 한다. 또한 배치정규화를 통해 딥러닝 모델을 학습시킬 때 더 빠르게 학습시킬 수 있는 다른 기법들은 무엇이 있는지 나열하고 논문을 마무리한다.




