| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- BOJ
- 추천시스템
- Noise Contrastive Estimation
- matrix factorization
- word2vec
- RecSys
- Skip-gram
- ANNOY
- wavenet
- SGNS
- 부스트캠프 AI Tech
- ALS
- Ai
- Negative Sampling
- CF
- Recommender System
- Collaborative Filtering
- Implicit feedback
- Dilated convolution
- CV
- Item2Vec
- Tacotron
- TTS
- 논문리뷰
- FastSpeech2
- Neural Collaborative Filtering
- Tacotron2
- NEG
- 백준
- FastSpeech
- Today
- Total
devmoon
NCF: Neural Collaborative Filtering 본문
ABSTRACT
2017년도 당시 딥러닝은 음성인식, 컴퓨터 비전, 자연어 처리 분야에서 뛰어난 성능을 보여주며 인기를 끌고 있었다. 하지만 추천시스템 분야에 대해서는 딥러닝이 많이 적용되거나 연구가 활발하게 이루어지지 않았다. 몇 가지 연구들이 추천시스템에 딥러닝을 적용시켜보기는 하였지만, 직접적으로 모델의 핵심 부분이 딥러닝으로 구성된 것이 아니라, 일부분만 딥러닝 연산을 사용하고 있었다. 따라서 딥러닝이 적용된 협업필터링(Collaborative Filtering)이더라도 여전히 두 잠재 벡터의 내적 연산은 필요했다.
저자들은 이번에 내적 연산의 문제점에 대해 소개하며 딥러닝 구조를 사용하여 내적 연산을 대체하도록 만들고자 했고 여러가지 실험을 통해 딥러닝을 핵심 부분으로 모델링하는 Neural network based Collaborative Filtering (NCF)를 발표하였다. 이 모델은 2종류의 데이터셋에 대해서 SOTA를 뛰어넘는 성능을 보여주었고, 모델의 레이어가 깊어질수록 성능도 올라가는 경향을 보여주었다고 발표하였다.
INTRODUCTION
추천시스템의 핵심은 유저들이 어떤 아이템들을 선호하는지 모델링하는 것이다. 협업필터링 중에서 Matrix Factorization은 유저와 아이템을 동일 공간에 임베딩시키는 것으로 선호도를 모델링한다. 이후에 유저와 아이템 잠재 벡터를 내적 하여 선호도를 측정하는 과정을 거치게 된다.
Netflix Prize 대회에서 유명세를 타게된 Matrix Factorization은 이후에 수많은 연구들이 이어졌다. 그러면서 협업필터링에서 MF는 효과적이라는 것이 알려졌지만, 동시에 "내적"이라는 연산 때문에 성능이 저해된다는 사실도 발표되었다. 예로, 내적연산에 Bias를 추가하기만 했을 뿐인데도 성능이 오른 연구가 존재하였다. 이는 내적연산이 유저와 아이템 사이의 상호작용 데이터를 정확하게 포착하기 어렵다는 의미로 해석할 수 있다.
따라서 저자들은 깊은 신경망 구조 (Deep Neural Networks, DNNs)를 내적연산을 대체하는데 사용하기로 하였다. 비선형성을 부여하여 더 복잡한 관계를 학습할 수 있을 것이라고 판단한 것이다. 물론 이전에도 DNNs를 추천시스템에 사용한 연구는 있었지만, 직접적인 학습을 하는데 신경망을 사용한 것이 아니라, 보조정보에 대해서만 DNNs를 사용하였다. 최종적으로 저자들이 이 논문을 통해 밝혀낸 것은 아래와 같다.
- 유저와 아이템의 잠재적 특징들을 NCF라는 프레임워크를 통해 학습시킬 수 있다.
- Matrix Factorization이 NCF의 일부임을 보이며, NCF는 다층퍼셉트론 구조를 사용하여 비선형성이 존재한다.
- 2개의 실생활 데이터셋을 사용하여 NCF가 효과적임을 보인다.
PRELIMINARIES
Learning from Implicit Data
$M$을 유저의 수, $N$을 아이템의 수라고 한다면, 상호작용 행렬을 $\mathbf{Y} \in \mathbb{R}^{M \times N}$ 으로 나타낼 수 있다. Implicit feedback은 상호작용 정보가 관측되었을 경우 1, 관측되지 않은 경우는 0으로 아래와 같다.
$$
y_{ui} = \begin{cases}
1, & \text{ if interaction (user u, item i) is observed} \\
0, & \text{ otherwise. }
\end{cases}
$$
Implicit Feedback의 특징으로 상호작용 정보가 1이라고 해서 유저가 해당 아이템을 선호한다는 의미는 아닌 것이다. 단지 상호작용 했다는 정보가 있어서 흥미가 있다고 유추할 수 있을 뿐, 확신을 가지고 이 유저는 저 아이템을 좋아한다라고는 할 수 없다. 반대로 상호작용 정보가 0이라고 해서 싫어한다는 의미는 아니며, 유저가 해당 아이템의 존재 자체를 몰라서 상호작용하지 못했을 수도 있다.
Implicit Feedback을 사용한 추천은 관측되지 않은 아이템(상호작용 하지 않은 아이템)들에 대해 선호도를 유추하여 랭킹을 매기는 작업과 같다. 수식으로는 $\hat{y}_{ui} = f(u, i \vert \Theta)$라고 표현한다. 여기서 $f$는 모델의 파라미터 $\Theta$를 사용하여 랭킹을 매기는 함수이며 상호작용 함수 (interaction function)를 가리킨다.
모델의 파라미터 $\Theta$를 추정하기 위한 방법으로는 크게 2가지가 있다. 하나는 pointwise loss, 다른 하나는 pairwise loss이다. 먼저 pointwise loss는 오차제곱을 최소로 하는 회귀와 같다. 예측값 $\hat{y}_{ui}$와 실제값 $y_{ui}$의 차이를 최소로 하도록 모델의 파라미터를 학습시키는 방법이다. pairwise loss는 관측된 아이템 $i$와 관측되지 않은 아이템 $j$ 정보를 사용하는데, 관측된 아이템이 관측되지 않은 아이템보다 선호한다는 것을 가정하고 출발한다. 따라서 학습할 때도, $\hat{y}_{ui} > \hat{y}_{uj}$가 되도록 학습을 시킨다.
Matrix Factorization
MF는 아이템 잠재벡터와 유저 잠재벡터의 내적으로 상호작용 정보를 예측한다. 수식에서 유저 잠재벡터를 $\mathbf{p}_u$, 아이템 잠재벡터를 $\mathbf{q}_i$라고 한다면, 예측 값은 아래와 같이 표현할 수 있다.
$$ \hat{y}_{ui} = f(u, i \vert \mathbf{p}_u, \mathbf{q}_i) = \mathbf{p}_u^\top \mathbf{q}_i $$
위의 내적연산은 선형연산으로 되어 있기 때문에 MF는 잠재 요인을 사용하는 선형모델이라고 간주할 수 있다. 아래의 사진은 Matrix Factorization의 표현력 한계를 보여주는 하나의 예시이다.

Matrix Factorization에서 유저와 아이템은 동일한 벡터공간에 임베딩되기 때문에, 유저 간의 유사도도 내적을 사용하는 코사인 유사도로 계산할 수 있다. 두 유저의 실제 유사도는 Jaccard 유사도를 사용한다고 가정하였다. 먼저 (a)에서 유저 1, 2, 3 사이의 유사도는 Jaccard 유사도로 $s_{23}(0.66) > s_{12}(0.5) > s_{13}(0.4)$로 나타낼 수 있다. 그렇다면, 벡터공간에서 (b)처럼 $p_2$와 $p_3$를 가깝게 그리고, $p_1$을 조금 떨어지게 그릴 수 있다.
문제는 여기에 새로운 유저 4가 들어왔을 때 발생한다. (a)에서 유저 4의 벡터 정보가 [1, 0, 1, 1, 1]이라고 한다면, 다른 유저와의 유사도는 $s_{41}(0.6) > s_{43}(0.4) > s_{42}(0.2)$가 된다. 다시 말해, 유저 4는 유저 1과 가장 가깝고 다음으로 유저 3, 마지막으로 유저 2가 가장 멀게 그려져야 한다. 하지만 이 조건들을 모두 만족하도록 벡터공간에서 유저 4를 그리는 것은 불가능하다. 유저 1과 가깝게 그리는 순간, 유저 2가 다음으로 가까워지기 때문이다.
물론 위의 문제는 벡터공간의 차원 $K$를 늘리면 해결될 수 있는 문제이다. 하지만 이 차원의 크기가 커질수록 과적합이 잘 일어나기 때문에 간단하게 늘릴 수만은 없다. 따라서 저자들은 이 부분에 DNNs를 사용하여 다루게 된다.
NEURAL COLLABORATIVE FILTERING
General Framework
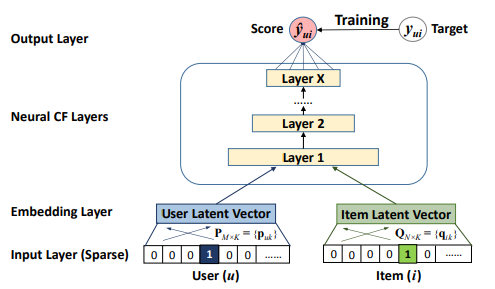
신경망 구조를 협업필터링에 사용하기 위해 저자들은 다층 구조를 모델링하도록 설계하였다. 모델의 첫 입력으로는 2개의 벡터가 주어지는데, 두 벡터는 각각 유저 벡터 $\mathbf{v}_u^U$와 아이템 벡터 $\mathbf{v}_i^I$이다. 이 벡터들은 원핫벡터로 구성되어 있어서 매우 희소(sparse)한 형태를 띠고 있다.
입력 레이어 다음은 임베딩 레이어로 희소한 유저 벡터와 아이템벡터를 dense한 형태로 변경해준다. 각각 임베딩 행렬을 참고하여 임베딩되며, 그 결과물을 임베딩 벡터라고 부른다. 유저 임베딩 벡터와 아이템 임베딩 벡터는 다음 레이어인 NCF 레이어로 전달되게 되는데, 이 레이어의 주요 역할은 유저와 아이템 사이의 상호작용 점수를 계산하는 것이다. 이후에 NCF레이어의 최종 출력인 $\hat{y}_{ui}$와 실제 점수인 $y_{ui}$간의 차이를 point wise loss로 계산한다.
Bayesian Personalized Ranking (BPR)과 같이 pairwise loss로 학습하는 것도 가능하지만, 저자는 나중의 일로 미루고 모델의 신경망 구조에 집중하기로 하였다. 이제 NCF를 수식으로 나타내보면 아래와 같다.
$$ \hat{y}_{ui} = f(\mathbf{P}^\top \mathbf{v}_u^U, \mathbf{Q}^\top \mathbf{v}_i^I \vert \mathbf{P}, \mathbf{Q}, \Theta_f) $$
- $\mathbf{P}$ : 유저 임베딩 벡터를 얻기 위한 유저 임베딩 행렬
- $\mathbf{Q}$ : 아이템 임베딩 벡터를 얻기 위한 아이템 임베딩 행렬
- $\Theta_f$ : 다층 신경망 구조에 사용되는 파라미터
$$ f(\mathbf{P}^\top \mathbf{v}_u^U, \mathbf{Q}^\top \mathbf{v}_i^I) = \phi_{out} (\phi_X ( \dots \phi_2 (\phi_1 ( \mathbf{P}^\top \mathbf{v}_u^U, \mathbf{Q}^\top \mathbf{v}_i^I )) \dots ))$$
- $\phi_{out}$ : 최종 출력 레이어
- $\phi_x$ : $x$ 번째 레이어
- $X$ : NCF 레이어의 수
Learning NCF
Neural Collaborative Filtering 모델 파라미터를 학습하기 위해 point wise loss를 사용한다고 했는데 여기서는 오차 제곱합 방법을 사용하였다. $\mathcal{Y}$ 를 상호작용이 관측된 (유저, 아이템)쌍이라고 하고, $\mathcal{Y}^-$를 상호작용이 관측되지 않은 (유저, 아이템) 쌍이라고 한다면 손실함수는 아래와 같이 정의된다.
$$ L_{sqr} = \sum_{(u, i) \in \mathcal{Y} \cup \mathcal{Y}^-} w_{ui} (\hat{y}_{ui} - y_{ui})^2 $$
- $w_{ui}$ : 하이퍼 파라미터인 학습 가중치
문제는, 이런류의 squared loss는 관측값이 정규분포를 따를 때 정의되는데, Implicit Feedback은 1 또는 0의 이진값으로 정의되기 때문에 잘 부합하지 않게 된다. 따라서 저자는 Implicit Feedback의 이진 특성에 초점을 맞추어, 확률적으로 point wise NCF를 학습하는 방법을 발표한다.
$\hat{y}_{ui}$를 $u$가 $i$를 얼마나 선호하는지 그 확률로 해석하기 위해서는 예측값이 0~1 사이의 값으로 출력되어야 한다. 0~1 사이의 값으로 제한하기 위해서는 간단하게 Logistic 함수나 Probit함수를 사용해 볼 수 있다. 일단 그전에 나올 수 있는 값이 0 또는 1로 베르누이 분포를 따르기 때문에 가능도함수는 아래와 같이 정의된다.
$$ p(\mathcal{Y}, \mathcal{Y}^- \vert \mathbf{P}, \mathbf{Q}, \Theta_f) = \prod_{(u, i) \in \mathcal{Y}} \hat{y}_{ui} \prod_{(u, j) \in \mathcal{Y}^-} (1 - \hat{y}_{ui}) $$
이 가능도 함수에 음의 로그를 씌워주면, Binary cross entropy loss와 같은 형태를 띄는 식을 구할 수 있다. 아래의 식이 목적함수가 되며, 경사하강법을 통해 파라미터를 최적화시키면 된다.
$$ \begin{align*} L &= -\log \ p(\mathcal{Y}, \mathcal{Y}^{-} | P,Q,\Theta_{f}) \\ \\ &= -\sum_{(u,i) \in \mathcal{Y}} y_{u,i} \log \ \hat{y}_{u,i} - (\sum_{(u,j) \in \mathcal{Y}^{-}} (1- y_{u,i}) \log \ (1-\hat{y}_{u,j}) ) \\ \\ &= -(\sum_{(u,i) \in \mathcal{Y} \cup \mathcal{Y}^{-} } ( y_{u,i} \log \ \hat{y}_{u,i} + (1- y_{u,i}) \log \ (1-\hat{y}_{u,i}))) \end{align*} \\ $$
Generalized Matrix Factorization (GMF)
이번에는 MF가 NCF의 하나의 케이스임을 밝힌다. 먼저, 임베딩된 유저와 아이템 벡터를 $\mathbf{p}_u, \mathbf{q}_i$라고 하고, 첫번째 레이어의 식을 성분곱으로 $\mathbf{p}_u \odot \mathbf{q}_i$라고 정의한다. 이제 여기에 가중치 $\mathbf{h}$와 활성함수 $a_{out}$을 곱해주면 NCF와 같은 형태를 띄게 된다.
$$ \hat{y}_{ui} = a_{out}(\mathbf{h}^\top (\mathbf{p}_u \odot \mathbf{q}_i)) $$
MF는 두 잠재벡터의 내적으로 상호작용 확률을 계산하는데, 위와 같은 NCF에서 활성함수가 Identity 함수이고, 가중치 벡터 $\mathbf{h}$의 원소가 모두 1이라면, MF와 정확히 동일한 연산을 수행하는 NCF가 된다. 이제 MF가 NCF의 일부임을 보였고, 성능을 강화하기 위해서 활성함수와 가중치 벡터를 적절히 설정해주면 비선형성도 갖게 되는 Matrix Factorization의 구현이 가능하다. 특히, 활성함수로 시그모이드 함수를 사용하고, 가중치 벡터를 log loss를 사용해 학습한 모델을 Generalized Matrix Factorization, 줄여서 GMF라고 칭하였다.
Multi-Layer Perceptron (MLP)
NCF에서 모델링할 때, 아이템 벡터와 유저 벡터에 대한 연산을 따로 진행했었는데, 하나로 이어 붙여서 연산하는 것이 더 직관적이다. 하지만, 단순히 이어 붙인다는 것이 둘 사이의 어떤 상호작용을 하도록 할 수 있는 것은 아니다. 이 문제를 해결하기 위해서, 이어 붙인 벡터에 대해서 hidden layer를 통과하게 만들어서 두 벡터 사이의 상호작용이 일어날 수 있도록 만들어 주었다.
$$ \begin{align*} \mathbf{z}_1 &= \phi_1(\mathbf{p}_u, \mathbf{q}_i) = \begin{bmatrix} \mathbf{p}_u \\ \mathbf{q}_i \end{bmatrix}\\ \phi_2(\mathbf{z}_1) &= a_2(\mathbf{W}_2^\top \mathbf{z}_1 + \mathbf{b}_2), \\ &\dots\dots\\ \phi_L(\mathbf{z}_{L-1}) &= a_L(\mathbf{W}_L^\top \mathbf{z}_{L - 1} + \mathbf{b}_L), \\ \hat{y}_{ui} &= \sigma(\mathbf{h}^\top \phi_L(\mathbf{z}_{L-1})) \end{align*} $$
이후에 또 다른 MLP 레이어를 통과시켜서 가중치 행렬과 곱 연산을 하고, bias를 더하여 활성함수를 거치게 만든다. 여기서 사용되는 활성함수로는 일반적으로 sigmoid, tanh, ReLU중 하나를 사용하는데, 결과적으로 ReLU가 tanh보다 조금 더 좋았고, sigmoid보다는 크게 성능을 앞질렀다고 한다. 또한 레이어의 차원에 대해서는 밑에가 넓고, 위로 갈수록 좁아지는 타워 형식이 가장 좋은 성능을 보여주었다.
Fusion of GMF and MLP
지금까지 GMF와 MLP에 대한 설명을 하고 그 예시를 하나씩 다 살펴보았다. GMF는 선형 연산을 통해서 두 임베딩 벡터 간의 상호작용을 모델링하고, MLP는 비선형 연산을 통해 두 벡터간의 상호작용을 모델링하였다. 하나 아이디어가 떠오르는 것은 GMF와 MLP를 적절히 섞어서 모델을 강화하고, 더 복잡한 상호작용을 모델링할 수 있지 않을까?이다.
간단하게 저자들은 임베딩 행렬을 GMF와 MLP가 공유하도록 하고, 임베딩된 벡터를 더해주는 방식을 떠올렸다. 하지만, 임베딩 행렬을 공유하게 되면, 두 차원을 일치하도록 맞춰줘야 하기 때문에 표현력에 제한을 걸 수도 있다는 단점이 존재하였다. 따라서 이를 개선시킨 새로운 모델인 Neural Matrix Factorization인 NeuMF를 소개한다.

NeuMF는 GMF와 MLP가 각각 별도의 임베딩 행렬을 갖게 되며 각 GMF, MLP레이어를 통과시킨 출력물을 concat시켜서 정답을 도출하는 모델이다. NeuMF의 구조를 그림으로 표현한 위의 사진을 보면, 각 임베딩 벡터를 GMF와 MLP레이어에 교차시켜서 넣고, 다시 결과를 concatenate하는 것을 볼 수 있다. 위 과정을 다시 수식으로 표현하면 아래와 같다.
$$
\begin{align*}
\phi^{GMF} &= \mathbf{p}_u^G \odot \mathbf{q}_i^G \\
\phi^{MLP} &= a_L(\mathbf{W}_L ^\top (a_{L-1}(\dots a_2(\mathbf{W}_2^\top
\begin{bmatrix} \mathbf{p}_u^M \\ \mathbf{q}_i^M \end{bmatrix} + \mathbf{b}_2)\dots))+\mathbf{b}_L)\\
\hat{y}_{ui} &= \sigma (\mathbf{h}^\top \begin{bmatrix} \phi^{GMF} \\ \phi^{MLP} \end{bmatrix})
\end{align*}
$$
Pretraining
딥러닝 모델을 학습할 때 파라미터가 적절히 초기화가 되었을 때, 좋은 학습성능을 보여준다는 것이 잘 알려져 있다. 따라서 NeuMF를 학습할 때도 파라미터 초기화를 신중히 해야 하는데, 저자들은 NeuMF가 두 모델이 합성된 형태임을 이용해서 각 모델을 학습시킨 파라미터를 그대로 사용하기로 하였다. 더 자세히, GMF를 학습시키고, MLP를 학습시켰을 때, 얻어지는 파라미터를 그대로 NeuMF에 사용한다는 의미이다.
차이점이 있다면, 출력층에서 가중치 행렬 $\mathbf{h}$를 생성할 때, GMF에서 생성한 것과 MLP에서 생성된 것을 적절히 섞어서 만들었다는 것이다.
$$ h \leftarrow \begin{bmatrix} \alpha \mathbf{h}^{GMF} \\ (1 - \alpha) \mathbf{h}^{MLP} \end{bmatrix} $$
GMF와 MLP를 학습시킬 때는 Adam Optimizer를 사용하였고, NeuMF를 사용할 때는 vanilla SGD를 사용하였다. 그 이유는 Adam이 파라미터를 적절히 업데이트할 때, momentum에 대한 정보를 필요로 하기 때문이다. 이미 적절히 초기화되어 있는데, 다시 momentum을 설정하여 학습하는 것은 적절하지 못하다고 판단하였던 것이다.
EXPERIMENTS
이번 파트에서는 다음 3가지 질문에 대한 실험 위주로 진행되었다.
- RQ1. 여기서 제안한 NCF 방법론이 기존 implicit feedback 데이터를 다루는 SOTA보다 더 좋은 성능을 내는가?
- RQ2. 여기서 제안한 최적화 기법이 추천에서 어떤 일을 하는가?
- RQ3. hidden layer가 많을 수록 유저와 아이템의 상호작용을 학습하는데 더 좋은가?
Experimental Settings
사용한 데이터셋은 MovieLens데이터셋과 Pinterest 데이터셋이다. 두 데이터셋의 상호작용 수, 아이템 수, 유저 수를 표로 정리하면 다음과 같다.
| 데이터셋 | 상호작용 수 | 아이템 수 | 유저 수 | 희소도 (Sparsity) |
| MovieLens | 1,000,209 | 3,706 | 6,040 | 95.53% |
| 1,500,809 | 9,916 | 55,187 | 99.73% |
평가를 위한 방법으로는 유저별 마지막 데이터셋을 남기는 leave one out 방식을 사용하였다. 모든 유저별로 모든 아이템에 대해 랭킹을 매기는 것은 시간소모가 매우 크기 때문에, 유저별로 100개의 랜덤 샘플링을 진행하고 순위를 매겼다. 성능을 Hit Ratio, NDCG로 평가하였다. NeuMF와 비교를 위한 모델로는 ItemPop, ItemKNN, BPR, eALS를 사용하였다.
저자들은 모델은 Keras를 사용하여 구현하였고, 모든 NCF모델들은 log loss를 최적화시키는 방향으로 학습되었다. 가장 초기에 모델들은 정규분포(평균 0, 표준변차 0.01)를 따르도록 초기화되었고 모델들은 Adam을 사용하였다. 배치크기는 128, 256, 512, 1024를 사용해 보았고, 학습률로 0.0001, 0.0005, 0.001, 0.005를 실험해 보았다. 마지막 레이어 차원의 크기는 8, 16, 32, 64로 실험을 했고, 더 커질수록 성능이 낮아지거나 과적합되는 경향을 보였다고 한다.
Performance Comparison (RQ1)

위 사진은 HR@10과 NDCG@10에 대한 성능을 보여준다. 먼저 가장 눈에 띄는 부분은 SOTA로 불리는 eALS 또는 BPR보다 두 데이터셋에서 더 나은 성능을 보여주었다. Pinterest는 예측 요소가 8로 적었음에도 불구하고, 큰 예측 요소인 64를 사용한 eALS나 BPR보다 지속적으로 좋은 성능을 보였다.
MLP와 GMF에 대해서 비교적 강한 성능을 보여주었는데 MLP가 살짝 아래에 나타나있는 것을 보인다. 하지만, MLP는 레이어를 추가하여 성능을 올릴 수 있기 때문에 1차원적으로만 바라볼 수 없다. 마지막으로 GMF는 BPR보다 거듭되는 성장을 보여주었고, 이는 log loss를 사용한 classification의 효율을 증명해 주었다. (둘은 동일한 MF 모델을 사용하였지만, 목적함수가 다름)
Log Loss with Negative Sampling (RQ2)

Implicit Feedback이 0과 1로 구성되어 있음에 따라 논문에서는 이를 binary classfication task와 같이 해결하였다. 논문은 NCF를 확률론적 모델로 보고 log loss를 통해 최적화를 진행하였다. 위의 사진 중 상단(Figure 6)은 loss의 변화를 말한다.
먼저 확인할 수 있는 것은 NCF는 iteration 수가 늘어날 때마다 loss 값은 줄어들고 성능은 향상되는 것을 볼 수 있다. 가장 효과적인 update는 초기 10번의 iteration에서 발생하였고, 더 많은 iteration은 over fitting을 야기시킬 수 있다. 그리고 NCF 방법론들 간에서 비교를 진행하면 성능 순서는 NeuMF, MLP, GMF 순이었다. 이를 통해 log loss를 통한 최적화가 implicit data 를 통해 학습하는데 효과적임을 보여준다.
Pointwise log loss를 pairwise 목적함수보다 사용하기 좋은 것은, 샘플링하는 비율을 조절할 수 있다는 것이다. 위의 사진에서 하단(Figure 7)을 보면 더 많은 Negative Sampling을 할수록 초반에 성능의 증가폭을 보임을 알 수 있다. 논문에서는 위의 실험결과를 통해 1개의 positive sampling 당 3~6개의 Negative Sampling을 진행하는 것이 최적이라고 발표하였다.
Is Deep Learning Helpful? (RQ3)

마지막으로 논문은 MLP에서 사용하는 hidden layer의 수가 많아지면 성능이 좋아지는지 확인하였다. 실험결과 layer가 점점 증가할수록, 성능이 올라감을 알 수 있다. 특히 MLP-0은 hidden layer가 존재하지 않아 임베딩된 벡터 간의 concatentation만 이루어진 상태를 말하는데, 이때는 특히 더 성능이 좋지 않은 것을 보아 단순 concatenation 보다 hidden layer를 통과시키는 것이 좋다는 것을 보였다.




